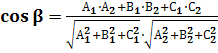Высшее назначение математики как раз и состоит в том, чтобы находить скрытый порядок в хаосе, который нас окружает. Норберт Винер

воскресенье, 20 апреля 2014 г.

IV этап


Команда "Апофемы"
Автор: на 1 комментарий:

Примеры с решением задач по тригонометрии от Лиги математиков

Примеры решения задач С1 и С2 с использованием тригонометрии.

Задача 1. а) Решите уравнение:

б) Найдите все корни уравнения, принадлежащие отрезку:
 Решение. а)Сначала заменим sin2x по формуле sin2x=2sinxcosx:
Теперь вынесем общие множители:
Видно, что можно вынести общую скобку (cosx-2):
Получили распадающееся уравнение, при котором каждую скобку необходимо приравнять к нулю. Первая скобка (cosx-2=0) не имеет решений, т.к. |cosx| не может быть больше 1, значит переходим к решению второй скобки:
Разделим каждый член уравнения на cosx и получим:
б) Отрезку  принадлежат корни  и  - это видно из окружности:
Ответ: а)  где , б)  и 
Задачу №1 подготовили Кукина Людмила и Ульянова Елена
Задача 2.
В комнате, имеющей форму куба, стоит телевизор, лежащий в плоскости EFF1. Найдите угол между окном, лежащим в плоскости DCC1, и телевизором, если известно, что E и F - середины сторон AB и CD соответственно.
Решение. Введем Декартову систему координат с началом в точке A и получим следующие координаты точек: D(1;0;0), C(1;1;0), D1(1;0;1), C1(1;1;1), E(0;0,5;0), F(0,5;1;0), E1(0;0,5;1), F1(0,5;1;1).
По рисунку видно, что плоскости пересекаются в точке E, значит можно искать угол между векторами AB и EF.
Координаты векторов найдем по формуле: 
Получим следующие координаты векторов: AB(0;1) и EF(0;0,5;0,5).
Теперь применим формулу косинуса между двумя векторами: 
Получим следующее выражение:
Значит угол между плоскостью окна и плоскостью телевизора: 45 градусов.
Ответ: 45 градусов.
Задача №2 была подготовлена Ахметзяновым Сергеем и Ленковским Игорем.
При создании блога были использованы ресурсы с сайтов festival.1september.ru и matematika-c1.ru
Автор: на 1 комментарий:

суббота, 19 апреля 2014 г.

Тригонометрия


Плакат по решению тригонометрических задач. Команда "Альфа" Новосанжаровская СОШ
Автор: на 5 комментариев:
Ярлыки: ,

воскресенье, 13 апреля 2014 г.

Стенгазета Лиги математиков по теме: "Решение задач на проценты".



Подготовлено с помощью ресурса.
Автор: на 3 комментария:

суббота, 12 апреля 2014 г.

                       Команда "Альфа" Новосанжаровская СОШ"
Автор: на 9 комментариев:

воскресенье, 6 апреля 2014 г.

Задача
На Олимпийских играх  по фигурному катанию в один из состязательных дней участвуют  :  спортсменок из России,  из США, 5 из Китая и 5 из Канады. Порядок, в котором выступают фигуристки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая последней, окажется из Китая.


Решение:

  1. Определим, сколько всего участвовало спортсменок в этот день n=8+7+5+5=25
  2. Давайте представим, что все спортсменки одновременно подошли к шляпе и вытянули из нее бумажки с номерами. Кому-то из них достанется двадцать пятый номер. Вероятность того, что его вытянет китайская спортсменка, равен 5/25 (поскольку из Китая —  спортсменок). 
Ответ: 0,2.


Команда "Бермудский треугольник"
Автор: на 3 комментария:

Всем кто любит хоккей, наверно, знакомо выражение: «Вратарь — это больше чем полкоманды». На ОИ в Сочи ворота нашей команды защищали 2 вратаря: Сергей Бобровский и Семён Варламов. В матче ¼ финала наша сборная играла со сборной Финляндии... и, к сожалению, проиграла 1-3. А основным вратарём был выбран Семён Варламов, а запасным Сергей Бобровский. Когда счёт в матче стал 3-1, тренерский штаб решил поменял вратаря.Давайте попробуем разобраться с математической точки зрения, прав ли был главный тренер команды Зинэтула́ Хайдарович Билялетди́нов в выборе основного вратаря на матч.

Условия задачи:
Сергей Бобровский выступает в NHL за клуб Columbus Blue Jackets.



Семён Варламов выступает в NHL за клуб Colorado Avalanche.



Статистические показатели вратарей:






Решение: 
              1.    сравним отношение побед каждого из игроков к общему количеству матчей:   
                     СБ=25/39=0,64103...
                     СВ=37/46=0,80435...
                     Вывод: отношение побед ко всем матчам лучше у С. Варламова.
    1. сравним отношение сухих матчей к общему числу матчей:
      СБ=3/39=0,07692...
      СВ=2/46=0,04348...
      Вывод: отношение сухих матчей к общему числу матчей лучше у С. Бобровского.

    2. теперь сравним отношение кол-во отбитых бросков к числу бросков за сезон:
      СБ=1046/1137=0,91996...
      СВ=1366/1477=0,90928..
      Вывод: отношение отбитых бросков ко всем лучше у С. Бобровского.

      Ответ: для выбора игрока на игру оказывает влияние множества факторов, но если брать ключевые показатели вратарей в течении сезона, то лучше они у Сергея Бобровского. Значит, с первых минут игры предпочтение нужно было отдавать как раз ему.

      При подготовке к задаче была использована информация с сайта:
      http://www.sports.ru/semen-varlamov/?type=stat
      http://www.sports.ru/bobrovsky/?type=stat
Автор: на 1 комментарий:

суббота, 5 апреля 2014 г.

Решение задачи по теории вероятности. Команда "Лига математиков".

Команда "Лига математиков"

Решение задачи по теории вероятности с олимпийским содержанием

"Во время национальных и международных соревнований проводится допинг-контроль не только призеров, но и остальных участников по жребию или выбору судьи по допингу. Помещения (станции) допинг-контроля размещаются на всех спортивных аренах. В большинстве видов спорта установленное применение допинга влечет за собой дисквалификацию на 2 года, а повторное — на 4 года или даже навсегда.
Однако многих спортсменов это не останавливает. Более того, большинство спортсменов употребляют допинг вне соревнований, на тренировках. При такой нагрузке это неудивительно. Тренеры же относятся к этому явлению весьма спокойно, и часто сами заставляют своих подопечных употреблять допинг.Официально заявляется, что тренеры не поощряют употребление допинга, а употреблять или не употреблять является личным выбором каждого спортсмена."
Статья из Википедии. 

ЗАДАЧА: 

На Олимписких играх в соревнованиях по биатлону в один день участвовали только 3 страны: Россия, Германия и Украина. Каждая страна предлагала по 2 участника. По статистике, которую мед. комиссия ведет с самого начала Олимпийских игр, вероятность отсутствия запрещенных препаратов в крови у российских спортсменов - 80%, немецких - 70%, украинских - 80%. Найдите вероятность того, что у спортсмена, выбранного случайно, на взятии проб крови не обнаружат "допинга".

РЕШЕНИЕ:

1. Обозначим Россию как 1 страну, Германию - 2 страну, Украину - как 3 страну.

2. Введем полную группу гипотез: 

Hi = (Вероятность того, что спортсмен из i-ой страны), тогда i =1,2,3.


3. Вычислим вероятности гипотез (отношение числа спортсменов из одной страны к общему числу спортсменов):
4. Введем событие А = (результат пробы допинг-контроля - отрицательный). По условию известны вероятности:
P(A|H1) = 0,8; - вероятность отсутствия запрещенных препаратов у спортсменов России
P(A|H2) = 0,7; - вероятность отсутствия запрещенных препаратов у спортсменов Германии
P(A|H3) = 0,8; - вероятность отсутствия запрещенных препаратов у спортсменов Украины
5. Вероятность события A найдем по формуле полной вероятности:

Ответ: 77%, или 0,77.

Идея для задачи была взята с данного сайта. 
Автор: на 7 комментариев:

2 этап. Команда "Апофемы"

Задача о пересечении независимых событий. 

Российская команда по керлингу на колясках завоевала серебро Паралимпиады-2014. И это повод для гордости за наших земляков! Именно поэтому наша команда решила взять в основу создания задачи это достижение. 

 
Команда "Апофемы"
Математика. Теория Вероятностей. Подготовка к ЕГЭ-2014. 
Ф.Ф.Лысенко, С.Ю.Кулабухов 
http://www.yuga.ru/news/325494/

Автор: на 7 комментариев:
Сводка недоступна. Нажмите эту ссылку, чтобы открыть запись.
Автор: на 9 комментариев:

пятница, 4 апреля 2014 г.

 Задача  команды "Альфа"МКОУ "Чебаклинская СОШ"

Решение:

Автор: на 7 комментариев:


http://ru.wikipedia.org/wiki/Россия_на_Олимпийских_играх


РЕШЕНИЕ

    Летние Олимпийские
 игры





Зимние Олимпийские 
игры
 
Места ( по сумме медалей) по годам
1908 – 14, 1912 – 15, 1952 – 2,
1956 – 1, 1960 – 1, 1964 – 1,
1968 – 2, 1972 – 1, 1976 – 1,
1980 – 1, 1988 – 1, 1992 – 1,
1996 – 3, 2000 – 2, 2004 – 2,
2008 – 3, 2012 – 3.
1956 – 1, 1960 – 1, 1964 – 1,
1968 – 2, 1972 – 1, 1976 – 1, 
1980 – 1, 1984 – 2, 1988 – 1,  
1992 – 2, 1994 – 1, 1998 – 3,
2002 – 5, 2006 – 4, 2010 – 11,
2014 – 1.
Таблицы распределения случайных величин X и Y занимаемых мест по сумме медалей по частотам М в летних и зимних Олимпийских играх
Х
1
2
3
14
15
Y
1
2
3
4
5
11
М
8
4
3
1
1
М
9
3
1
1
1
1
N = ΣM = 17
N = ΣM = 16
Соответствующие упорядоченные ряды.
1, 1, 1, 1, 1, 1, 1, 1,2, 2, 2, 2, 3, 3, 3, 14, 15
1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 3, 4, 5, 11
СРАВНИМ ПРЕДЛОЖЕННЫЕ СОВОКУПНОСТИ ПО СЛЕДУЮЩИМ ХАРАКТЕРИСТИКАМ.
1.      Найдем размах R между наибольшими и наименьшими значениями случайных величин.
R = 15 – 1 = 14
R = 11 – 1 = 10
Вывод: можно сказать, что размах по местам в летних Олимпийских играх больше, чем в зимних Олимпийских играх.
2.      Определим моду М0 – наиболее часто встречающиеся значения
случайных величин X и Y.
М0 = 1
М0 = 1
Вывод: на летних и зимних Олимпийских играх преимущественным является 1 место.
3.      Найдем медиану Ме  - серединное значение упорядоченного ряда
случайных величин X и Y.
N = 17 – нечетное число. Его медиана равна значению центрального девятого члена упорядоченного ряда.
Ме = 2
N = 16 –четное число. Его медиана равна среднему арифметическому двух центральных значений восьмого и девятого членов упорядоченного ряда.
Ме = ( 1 + 1) : 2 = 1
 

ВЫВОД: сравнивая результаты характеристик, можно сделать вывод, что команда России  сильнее в зимних Олимпийских играх.









Автор: на 10 комментариев:
Подписаться на: Сообщения (Atom)